Pourquoi certains affirment que 2+2=5… et pourquoi ils ont peut-être raison

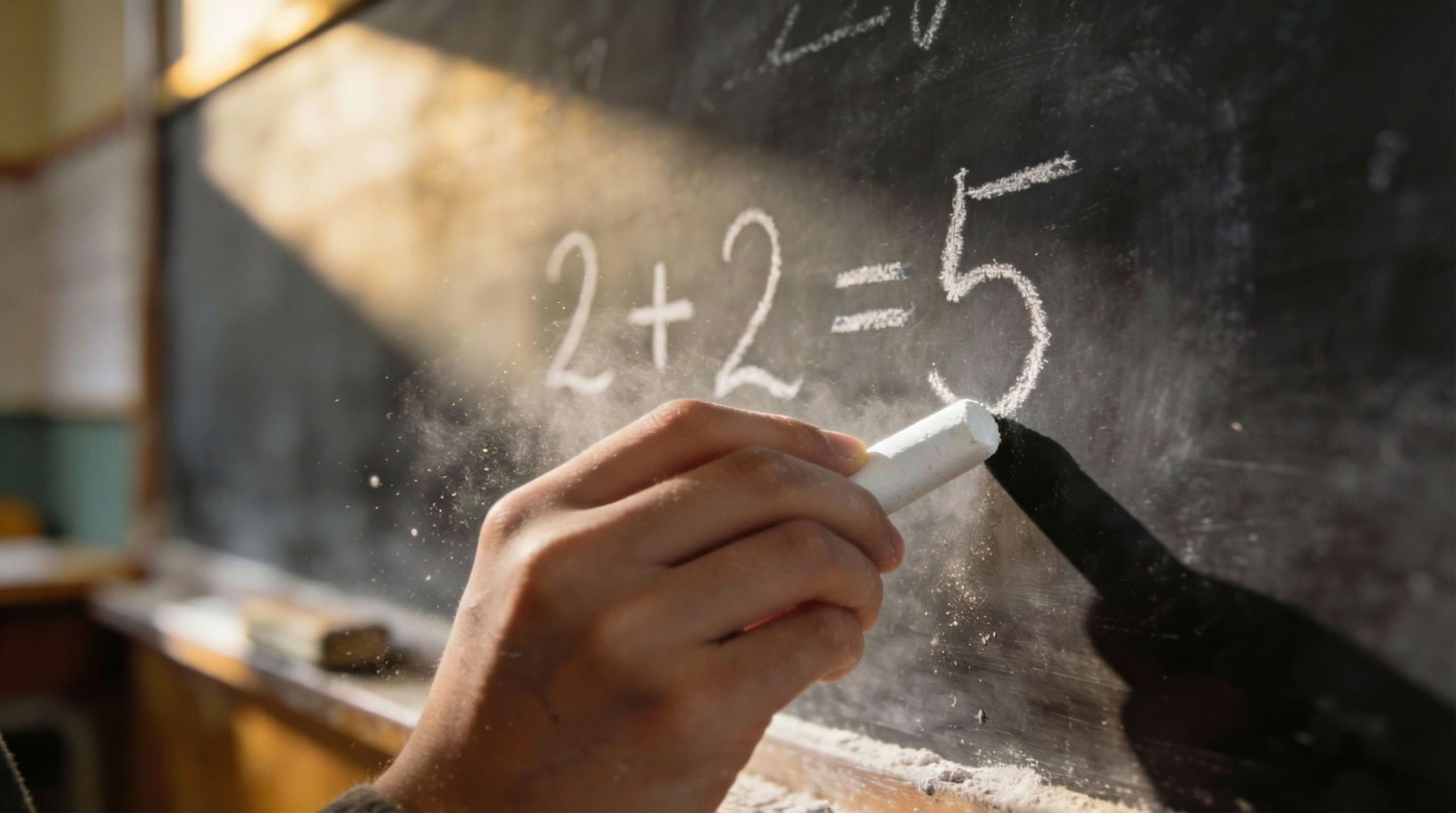
Quand le contexte change la donne

Sur le papier, c’est probablement l’un des problèmes mathématiques les plus simples au monde : 2+2. Si vous comptez quelque chose de tangible, comme des vis dans une quincaillerie, le résultat est assez simple et indiscutable. Mais, voyez-vous, les lignes deviennent floues dès que l’on change de contexte. Imaginez un instant… Si vous ajoutez 2 tasses de vinaigre à 2 tasses de bicarbonate de soude, la réaction chimique produit 5 tasses d’un mélange gazeux et mousseux. Est-ce que cela signifie pour autant que 2+2=5 ? C’est là que ça devient intéressant.

Nous apportons constamment des hypothèses dans le monde des mathématiques sans même nous en rendre compte. Dans ce cas précis, les simples « nombres entiers » — 1, 2, 3, et ainsi de suite — marquent un véritable fossé entre l’abstraction des maths et leur application réelle. En utilisant l’équation « 2+2=4 » comme matière à réflexion, les mathématiciens explorent les circonstances étranges où 2+2 ne fait pas vraiment 4, du moins pas proprement. Et je pense qu’on peut étendre ces interprétations à des questions bien plus larges en épistémologie — c’est-à-dire, comment savons-nous ce que nous savons ? C’est fascinant, non ?

Il y a quelques années, Kareem Carr, un étudiant en doctorat de biostatistique à l’Université de Harvard, a déclenché un débat houleux sur ce fameux « Est-ce que 2+2 vaut parfois 5 ? » sur la plateforme X, anciennement Twitter. C’était le 30 juillet 2020. Il a écrit quelque chose qui a fait réagir beaucoup de monde : « Je ne sais pas qui a besoin d’entendre ça, mais si quelqu’un dit que 2+2=5, la réponse correcte est : ‘Quelles sont vos définitions et vos axiomes ?’ et non une diatribe sur le déclin de la civilisation occidentale ». Dans son fil de discussion, Carr a souligné que les nombres sont des abstractions de choses réelles sous-jacentes dans l’univers, nous devons donc être conscients de la façon dont ces abstractions peuvent parfois déformer la vérité lorsqu’elles sont introduites dans des scénarios du monde réel.

Les pièges de l’abstraction : Vis, angles et arrondis

L’arithmétique fonctionne à merveille dans un manuel scolaire, c’est certain. Mais dans la pratique ? Elle se heurte souvent à des questions contextuelles qui ne tiennent pas compte des parties d’un tout, des approximations ou de vecteurs plus pertinents. Prenons un exemple concret, un peu technique mais éclairant. Si vous ajoutez des degrés entiers à un angle, vous finirez éventuellement par faire le tour complet pour revenir à un angle qui mesure 360 degrés. Mais voilà le hic : un angle de 360 degrés a exactement la même orientation qu’un angle de 0 degré. Donc, que l’angle mesure 0 ou 360 dépend entièrement du contexte. De même, si vous avez vissé une vis de cinq rotations complètes (soit 1 800 degrés) au lieu de quatre (1 440 degrés), l’orientation de la tête de la vis reste la même, certes, mais dans un cas, elle est enfoncée bien plus profondément dans le bois. C’est une nuance cruciale.

Le tweet de Carr a reçu des réponses montrant d’autres exemples des limites réelles de l’arithmétique, et franchement, certains font réfléchir. Beaucoup de gens ont souligné que deux animaux peuvent devenir trois par la reproduction (donc 1+1=3, ou même 1+1=1 selon vos paramètres de comptage), ou que deux machines pourraient devenir trois machines si vous aviez quelques pièces de rechange de chacune et un peu d’huile de coude. D’autres, plus pointilleux, ont noté que 2,3 s’arrondit à 2, n’est-ce pas ? Mais si on fait l’addition avant : 2,3 + 2,3 donne 4,6, ce qui s’arrondit à 5. Cela rend possible, à travers un certain filtre mathématique, que 2+2=5. C’est troublant.

En général, l’idée que nous apprenons de manière innée à compter les nombres — des valeurs entières uniquement, sans fractions ni décimales — est une idée fausse courante chez les gens qui ne sont pas formés en maths ou en développement humain. Les jeunes enfants apprennent les nombres un par un, en comptant, mais ne commencent à apprendre un comptage plus sophistiqué que lorsqu’ils peuvent reconnaître les quantités rapidement, une capacité appelée la subitisation. Il devient plus facile pour nous de compter jusqu’à 7, par exemple, lorsque nous pouvons reconnaître un groupe de quatre choses et ensuite compter la cinquième, la sixième et la septième. Compter est une compétence apprise, pas naturelle — même les animaux non humains qui peuvent « compter » jusqu’à quatre ou cinq, comme les chiens et les chimpanzés, sont considérés comme exceptionnels. Imposer des nombres abstraits au monde réel crée donc une tension innée.

Statistiques, politique et histoire : Quand les chiffres mentent

Il y a d’autres problèmes avec l’abstraction des mathématiques sur papier, et c’est là que ça devient sérieux. Carr ancre son concept de « 2+2=5 » dans les manières dont les modèles statistiques peuvent causer du tort à des groupes marginalisés selon certains paramètres. Il explique : « Chaque fois que vous créez une construction numérique comme le QI, ou un score d’agression, ou un score de sentiment, il est important de se rappeler que les propriétés de ce score pourraient ne pas refléter les choses réelles mesurées ». Le score de sentiment, par exemple, est le moyen principal par lequel les entreprises analysent les avis pour détecter un « sentiment » positif ou négatif, tandis que les échelles d’agression sont utilisées pour évaluer les patients psychiatriques. Dans chaque modèle, les gens doivent attribuer des valeurs numériques arbitraires (sur une échelle de 1 à 10, disons) à un critère qui n’est pas tangiblement mesurable. Carr précise : « Quand vous essayez de créer une construction statistique d’un phénomène mental, mon sentiment pourrait changer d’un moment à l’autre ». C’est dur de noter ses sentiments quand ils changent autant, ou quand le minimum ou le maximum de l’échelle n’est pas facilement concevable par notre expérience.

Bien que le débat de Carr autour de « 2+2=5 » soit quelque peu postmoderne par nature, l’équation a un passé chargé en tant que principe de l’anti-intellectualisme. C’est assez historique, en fait. Par exemple, Fiodor Dostoïevski a mis en scène le protagoniste sans nom de son roman de 1864, Les Carnets du sous-sol, pour qu’il croie que 2+2=5. Dostoïevski musait qu’une telle objection à la logique externe représente le libre arbitre qui rend une personne humaine. D’un autre côté, George Orwell, dans un essai de 1943, décrivait la propagande nazie comme un déni de la science, notant que si Hitler proclamait que « deux et deux font cinq », cela serait reçu comme la seule vérité certaine. Orwell a répété cette idée obsédante dans son roman 1984.

Conclusion : Au-delà de la certitude

Certains critiques de mauvaise foi ont inondé les mentions de Carr, affirmant que la valeur des maths réside dans leur fiabilité et leur rigidité. Mais la réponse de Carr pointe vers la distinction entre utiliser les maths comme un outil pour trouver des réponses et les utiliser comme un outil pour apprendre. Il dit, et je trouve ça très juste : « Il y a beaucoup de gens qui cherchent les maths et les statistiques pour un sentiment de certitude : ‘Ceci est la réponse’. Et il y a des gens qui ferment leur esprit. Je suis plus de l’autre côté : Y a-t-il autre chose que je pourrais découvrir dans ce complexe d’idées ? C’est le frisson de la découverte, comme quand les gens font de la détection de métaux ».

Finalement, Carr affirme qu’élargir la conception des gens sur les avantages et les inconvénients de diverses applications mathématiques mènera à une pensée critique plus profonde sur la façon dont les maths croisent nos vies. « Il y a un besoin pour ce genre de pensée, parce que nous transformons essentiellement tout en données », dit-il. Les films ont des « Tomato-meters », les podcasts ont des classements par étoiles, et les réseaux sociaux regorgent de ratios. Si nous devons être un monde qui n’existe que dans des applications, nous devons être sûrs que ces choses fonctionnent comme nous pensons qu’elles fonctionnent.

Ce contenu a été créé avec l’aide de l’IA.